|
欧米を中心とした速記と同様、 日本語速記においてもいわゆる 「正円幾何派(以下、幾何派とする)、 草書派、文字派」といった分類がある。 この場合の「派」というのは、当該速記方式 (≒流派)で用いられる速記符号(直線や曲線など)の形状がどのような由来、属性を持つのかといった意味での「派」ということになる。 これら3とおりの「派」についての説明を以下に掲げる。 ◆正円幾何派=幾何派 (Geometric systems) ・・・主に定規とコンパスにより書かれる線を理論上の書線としてとらえる。 円弧(円の一部)や数方向の直線、円、楕円、点、等々によって構成される。 フランス語、イタリア語、スペイン語、ポルトガル語といったラテン語系統の言語、英語、日本語、韓国語、中国語などに、「幾何派」に相当する速記法が数多く存在する。 ◆草書派=斜線派=斜体派 (Cursive systems) ・・・ローマ字の筆記体のような線を速記符号として用いる。草書派の速記法には、 母音に「右上方向、水平方向」などの上昇傾向の書線を多く用い、子音に「左下方向、右下方向、水平方向」などの下降傾向の書線を多く用いるものが多い。ヨーロッパ諸言語にはこれに相当する速記法も数多く存在する。ドイツ語やオランダ語、北欧の諸言語、中欧や東欧の諸言語、ロシア語などのスラヴ系言語などでは「草書派」がかなり優勢で、ほぼ席巻している状態である。 ◆文字派 (Alphabetic systems) ・・・普通文字の一部を速記の書線に用いる。また、文字派以外の速記書線をも実際には用いたりする。この「文字派」に相当する速記法は、上記の「幾何派」や「草書派」が存在する各言語の多くに結構存在するようである。なお、英文速記のGregg 式のように、「幾何派」に「草書派」を一部融合させたような書線を有するため、「半草書派=半斜線派=半斜体派」(Script-Geometric shorthand または Semi-Script shorthand)などと分類できるものもある。
さて、ここからは日本語速記において圧倒的に優勢で、ほぼ席巻している状態であるところの「幾何派速記)」で用いられる「幾何派速記符号」の形状等について、速記を学ばれたことのない一般の方々にもできるだけ理解しやすい表現で語りたいと思う。 日本語速記の4大方式と言われる方式の中から、民間方式としてともに著名な「中根式」と「早稲田式」を例に、「ナ、ニ、ヌ、ネ、ノ」の速記符号を以下に掲げる。 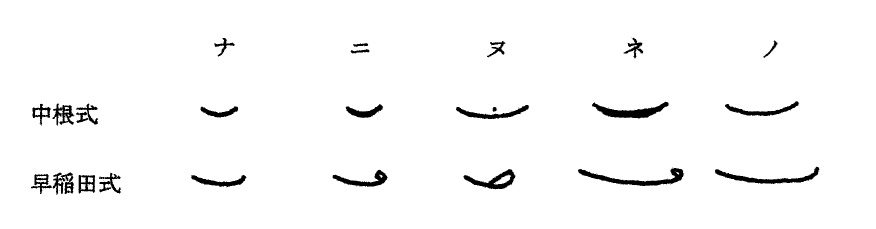
中根式及び早稲田式の「ナノ」 のような線を 「単画線」と呼ぶ。 また、早稲田式の 「ニ、 ヌ、ネ」のように、単画線に円等々 (その他フックなどがあり得る)が付された線を 「複画線」と呼ぶ。 書記動作上、単画線も複画線も1画に違いないが、1本の髪の毛のように 直線や曲線」のみで書かれるもの (円などのサインを伴わないもの) を、日本では速記方式の発達史上、単画線として分類したりする。 「幾何派、草書派、文字派」という分類とは別に、以下に掲げる 「複画方式(複画派)、単画方式(単画派)、折衷方式(折衷派)」 といった分類が日本語速記には存在する。 ◆複画方式 (複画派)・・・五十音符号の全てが複画線である場合、 複画方式と呼ばれる。 なお、いわゆる原始田鎖式のように、母音やア列子音に充てられる符号が単画線であっても、方式発展史上、「複画方式」に分類される場合もある。 ◆単画方式 (単画派)・・・五十音符号の全てが単画線である場合、単画方式と呼ばれる。 ◆折衷方式(折衷派)・・・五十音符号に複画線と単画線が混在する場合、折衷方式と呼ばれる。 単画線のみの構成を持つ中根式は単画方式とされ、単画線と複画線が混在する早稲田式は折衷方式とされている。 日本の符号式手書き速記の始まりとされる田鎖綱紀によるいわゆる田鎖式の速記符号は複画方式としてスタートした。 そして、その弟子である 「若林玵藏、酒井昇造、林茂淳」 らによる改良進化により本格的な実用化が図られた。 その後も、衆参両院の速記方式である参議院式 (貴族院式)や衆議院式の速記者養成所での改良進化を初め、 田鎖系複画方式を用いる往年の実務家らにより多様な案が示され、 明治、大正、昭和という時代を通して複画方式は逞しく生き続けた。 4大方式中の参議院式も衆議院式も、当初はいわゆる田鎖式系統の符号 (複画方式) から教授が始められ、長い年月の間に改良進化の道をたどってきた。 ちなみに複画方式で教授された最終年(養成所入所年)は、参議院式が1949年(昭和24年)、衆議院式が1938年(昭和13年)である。 両式とも「複画方式、単画方式、折衷方式」のいずれをも経験しているが、最新式 (最終式)のものとしては、参議院式が折衷方式で衆議院式は単画方式であるということも極めて興味深い。 これら方式も含めたところの現存する方式(現在でも学ばれている、もしくは使用されているとされる方式) は、少なくとも幾何派に分類される方式としては複画方式はおよそ見当たらないと言ってよく、単画方式と折衷方式が共存している状態である。 |